Geschicktes Rechnen mit Längenmaßen
Viele Schüler haben Schwierigkeiten bei der Umrechnung von Längen- und Flächenmaßen. Ich kenne das auch noch von früher: Man wusste nie, durch was denn bei der Umrechnung von cm² in m² geteilt werden muss. Bzw. man hat es nur so gelernt: Quadratzentimeter in Meter, geteilt durch 10000. Dabei ist dieses sture Pauken ohne die Zusammenhänge zu verstehen absolut uneffektiv, denn sobald sich nur die Größenordnungen ändern, steht man wieder im Wald.
Wenn man sich aber einmal mit diesen Maßen richtig beschäftigt, kann man eine Technik entdecken, welche nicht nur universell funktioniert, sondern auch einfach nur elegant ist.
Zuerst einmal schauen wir uns die Abkürzung cm genauer an. Für was stehen denn die beiden Buchstaben? Die Einheit Meter wird immer durch das m definiert. Der Buchstabe davor ist eigentlich eine Zahl und gibt eine Größenordnung an. Verbunden sind die beiden durch einen Malpunkt. c steht hierbei für Zenti und ist ein Vorsatz für Maßeinheiten. Damit vermeidet man lange Zahlen, indem man die Nullen salopp gesagt in die Abkürzung packt. Das c könnte man also auch als 0,01, 1/100 oder am Geschicktesten als 10^(-2) schreiben.
An dieser Stelle hat man nun schon was ganz Wesentliches gelernt. Um Längenmaße egal welcher Gestalt (z.b. cm oder km) in Meter umzurechnen reicht es, einfach diesen Vorsatz als Zahl zu schreiben und bei Bedarf eben ein wenig zu rechnen. Aus 5000 cm ergeben sich so 5000 * 0,01 m , was genau 50 Meter entspricht. Natürlich muss man dazu die Vorsätze und ihre Wertigkeit kennen. In der Wikipedia gibt es eine ausführliche Liste dazu. Ausdrucken, an die Wand neben dem Schreibtisch hängen und nach ein paar Mal rechnen hat man die drauf.
Aber wie funktioniert die andere Richtung? Wie kommt man von Meter auf Millimeter? Klar, man könnte erst mit 100 malnehmen(m --> cm) und dann noch mit 10. Aber wir wollen es gleich richtig lernen. Millimeter (mm) ist ja nichts anderes als 0,001 * m. Milli steht für Tausendstel. Wie bekommt man nun in den Ausdruck 1 m diesen Faktor Milli rein? Ganz einfach: Wir fügen eine nahrhafte Eins ein. In jedes Produkt dürfen ja beliebig viele 1er hineingeschrieben werden. 5*6 ist genau dasselbe wie 1*5*1*6*1. Damit die eins "nahrhaft" wird, was soviel bedeutet wie nutzbar, kann man sie auch als Bruch schreiben, mit identischem Zähler und Nenner. Das sieht dann so aus:
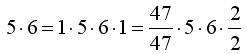
Alles genau dasselbe, oder? In diesem Fall ein blödes Beispiel, aber für unser Maßeinheitenproblem macht das verdammt viel Sinn:
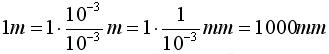
Wir fügen die nahrhafte Eins ein, wandeln das 10^(-3) im Zähler in Milli um und rechnen die restlichen Zahlen aus. Natürlich muss man sich ab dieser Stelle mit den Potenzgesetzen auskennen. Wer noch nicht soweit ist fügt eben statt 10^(-3) 0,001 im Zähler und Nenner ein, das ist genau dasselbe.
Das ist eigentlich schon der ganze Trick. Durch geschicktes Einfügen von nahrhaften Einsen kann man Längeneinheiten so umformen, wie man es gerne möchte. Um von Millimeter zu Kilometer zu kommen muss eben mit 10^6 / 10^6 erweitert werden. So bildet sich im Zähler das Kilo und im Nenner bleibt ein 10^6. Euer Lehrer würde hier sagen: "Durch eine Million teilen". Daher kommen nämlich auch diese ominösen Faktoren zum Umrechnen, welche man sonst immer auswendig lernen musste.
Exakt gleich funktioniert auch das Umrechnen von Flächen- und Volumenmaßen. Hier gibt es nur einen kleinen Fallstrick, eine ungenaue Schreibweise, welche oft für Verwirrung sorgt: cm² steht ja für Quadratzentimeter. Das Quadrat bezieht sich an dieser Stelle aber nicht nur auf die Meter, sondern auch auf das Zenti. Korrekterweise müsste man also (cm)² schreiben, was identisch zu c² * m² ist. Nun kann man wieder wie oben verfahren: Nahrhafte 1 einfügen, um den gewünschten Vorfaktor zu bilden, restliche Zahlenwerte ausrechnen. Aber Achtung: Auch hier muss das Quadrat wieder berücksichtigt werden. Um (km)² zu bilden, muss ein Faktor 10^6 im Term geschaffen werden.
Ein Beispiel hierzu:
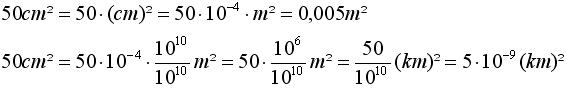
Das ist alles. Nun seid ihr bestens gerüstet für alle Arten von Längen-, Flächen- und Volumenumrechnungen.
Geschrieben am 03.06.2007 von Stefan
Kommentare
Noch keine Kommentare vorhanden
Kommentar hinzufügen
